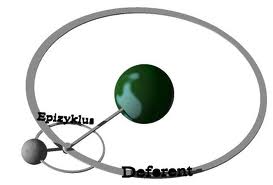
APOLONIO DE PERGA

Apolonio de Perga o Perge (262 a.J.C. - 180 a.J.C.) Matemático griego. Conocido con el sobrenombre de el Gran Geómetra, sus extensos trabajos sobre geometría tratan de las secciones cónicas y de las curvas planas y la cuadratura desus áreas. Acuñó los términos elipse, hipérbola y parábola,que responden a las respectivas propiedades matemáticas de estas tres funciones. También explicó el movimiento de los planetas según la teoría de los epiciclos.

Apolonio vivió largo tiempo en Alejandría, primero como discípulo y más tarde como profesor en la escuela de los sucesores de Euclides, escuela que recibió nuevo impulso del mismo Apolonio. Realizó numerosos viajes y residió también durante algún tiempo en Éfeso y en Pérgamo, a cuyo rey Atalo I (224-197) dedicó el cuarto libro de su tratado sobre las figuras cónicas. 

Apolonio hizo con respecto a las figuras cónicas, lo que Euclides había hecho un siglo antes en cuanto al círculo, y fue él quien dió a las secciones del cono las denominaciones todavía en uso: parábola, hipérbola, elipse. Aunque sólo cuatro de los ocho libros de que estaba compuesto hayan llegado a nosotros en la lengua original (poseemos otros tres en idioma árabe), el tratado es tan completo que habían de pasar siglos antes de que pudiera añadirse algo sobre el tema.

Ya antes de Apolonio, las cónicas y sus propiedades eran conocidas por los griegos, según lo atestiguan la obra de Menecmo, Los lugares sólidos de Aristeo y muchos pasajes de Euclides y Arquímedes. Apolonio generalizó y extendió las investigaciones. Partiendo de un cono cualquiera, cortándolo con un plano cualquiera, llega a obtener las tres especies de cónicas que antes de él se consideraban como secciones del cono acutángulo, rectángulo y obtusángulo.

Los primeros cuatro libros del tratado, Las cónicas han llegado a nosotros en su texto original porque probablemente eran libros de texto en las escuelas griegas y alejandrinas. Los tres siguientes se conservaron durante el medioevo en una traducción árabe, y sólo el octavo libro, que según las declaraciones de Apolonio contenía la solución de los problemas concernientes a la materia tratada en el libro anterior, se ha perdido. El famoso astrónomo Halley, en la edición hecha por él de las obras de Apolonio (1710), se basó en las informaciones contenidas en los "lemas" dejados por Pappo en su Colección para dar una relación aproximada de este libro desaparecido.

E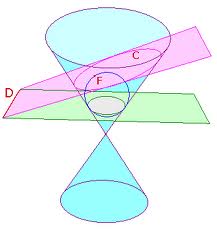n conjunto, los libros sobre las cónicas pueden considerarse como una introducción a la Geometría superior, porque en ellos encontramos nociones modernísimas como son los principios de la teoría de las polares o la generación de una cónica mediante haces de rayos proyectados (teorema de Steiner). La importancia de las cónicas en el sistema universal creció mucho con el descubrimiento de Kepler, según el cual las órbitas planetarias son elípticas, ocupando el sol uno de los focos de la elipse. La obra de Apolonio, al reexaminarse hace tres siglos, dió origen a un gran desenvolvimiento de la Geometría moderna.

Además de este libro, escribió otras obras sobre matemáticas, han llegado a nosotros, en versión árabe, dos libros sobre Divisiones de las proporciones, una obra sobre Tangencias y dos libros sobre Lugares planos. Entre los escritos perdidos se conocen los títulos de una obra sobre Resolución rápida y otra sobre espejos ustorios. Después de Arquímedes, Apolonio de Perga es el más profundo y original de todos los matemáticos griegos. Los antiguos le atribuyeron la invención de una forma especial de reloj solar y descubrimientos astronómicos precursores.

Curvas cónicas

Son curvas planas de segundo grado. También se les llama Secciones Cónicas, porque son el resultado de intersectar con un plano un cono de revolución. Las curvas cónicas propiamente dichas son tres: Elipse, Parábola e Hipérbola, aunque alterando el cono o la posición del plano pueden buscarse otras figuras, entre ellas la circunferencia.

• Focos: son los puntos de contacto de la sección con las esferas tangentes al plano que la produce e inscritas en el cono. 

• Diámetro: rectas que pasan por el centro geométrico. 

• Dos diámetros son conjugados cuando cada uno pasa por la polar del otro. 

• Ejes: mayor (o focal) y menor. Son los únicos diámetros conjugados perpendiculares. 

• Vértice: cualquier punto del eje mayor sobre la curva. 

• Circunferencia focal: de radio igual al eje mayor, y centro en uno de los focos. En la Parábola el elemento correspondiente es la recta Directriz. 

• Circunferencia principal (o circunscrita): tiene como diámetro el eje mayor. Una recta tangente a una elipse se corta en ella con las perpendiculares que se tracen desde los focos. 

• Radios vectores: segmentos que unen un punto de la curva con los dos focos.

Elipse
 

Es el lugar geométrico de los puntos de los que la suma de distancias a otros dos fijos es constante (los puntos fijos son los focos, y la suma de distancias es igual al diámetro mayor)También es el lugar geométrico de los centros de las circunferencias tangentes a otra dada que pasan por un punto interior a esta, o de los puntos que equidistan de una circunferencia y de un punto interior.

Parábola

Es una curva plana, abierta y de una rama. Se define como el lugar geométrico de los puntos que equidistan de otro punto y de una recta (Foco y recta Directriz). Puede compararse a una elipse en la que uno de los focos se desplaza al infinito. La recta Directriz corresponde a la circunferencia focal. Puede construirse cortando con arcos desde el foco rectas paralelas a la directriz, tomando como radio la distancia a ésta de cada una de las paralelas. También por cruce de proyecciones si conocemos el eje, el vértice y un punto P de la curva, o definirla uniendo el foco con distintos puntos de la tangente principal y trazando desde estos puntos rectas perpendiculares, que serán tangentes a la curva.

Hipérbola

La Hipérbola es una curva plana, abierta y con dos ramas. Es el lugar geométrico de los puntos de los que la diferencia de distancias a otros dos fijos es constante. También es el lugar geométrico de los centros de las circunferencias tangentes a otra dada que pasan por un punto exterior a ésta, o de los puntos que equidistan de una circunferencia y de un punto exterior. La medida nominal del eje mayor sigue siendo la distancia entre los vértices A e B de la curva. Las asíntotas son las tangentes de la curva en el infinito. Dependiendo de los datos, su construcción se hace por métodos esencialmente iguales a los empleados en las otras curvas cónicas.

Propiedades de las curvas cónicas

Cualquier recta trazada desde un foco a una elipse será reflejada en dirección al otro foco.En la parábola todos los reflejos serán paralelos al eje.  Así, las antenas parabólicas permiten la emisión o recepción unidireccional de las ondas.

En la hipérbola, los reflejos formarán un haz divergente polarizado por el foco contrario. Las estructuras convexas basadas en curvas cónicas  presentan una muy  buena resistencia a las presiones exteriores, siendo utilizadas, entre otras cosas, en la construcción de arcos y puentes.

Tangentes y normales

Tangente y normal en un punto P de la curva: son las bisectrices de los ángulos producidos por las rectas que pasan por P y por cada uno de los focos. Su posición en la Hipérbola es inversa que en la Elipse.

En la parábola se considera el segundo foco en el infinito.