Aristarco (310 a. C. – 230 a. C) nacido en Samos, Grecia, fue uno de los grandes astrónomos griegos del cual se perdió la mayor parte de su trabajo, seguramente en el incendio de la Biblioteca de Alejandría, con lo que no se guarda mucho más que cartas o menciones que hacían de él otros contemporáneos.
Pese a esto, se conoce que pudo ser uno de los más grandes genios que han podido existir, ya que con unas pocas medidas pudo obtener un gran conocimiento sobre el Sistema Solar (publicado en su obra “Sobre los tamaños y distancias del Sol y de la Luna“), hasta llevarle finalmente a la conclusión de que la Tierra no debía de estar en el centro, sino que debíamos de girar nosotros en torno al Sol, y no al revés (publicación que se perdió pero quedaron las cartas de sus contemporáneos donde se le criticaba por dichas ideas), lo que le llevó a obtener un gran número de críticas en su época y que sus ideas no se tuvieran en cuenta, hasta que finalmente, casi 2000 años después, Copérnico publicó el modelo heliocéntrico.
A continuación, daremos un repaso sobre cómo encadenó sus ideas y mediciones para llegar a los resultados a los que llegó. Eso sí, algunos de los procedimientos no se ciñen exactamente a cómo los realizó él, aunque siguen los mismos fundamentos para llegar a las mismas conclusiones.
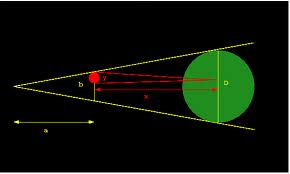Comencemos por una de las pocas medidas que tuvo que realizar Aristarco. Valiéndose de anteriores estudios, Aristarco apoyaba la idea de que cuando la Luna está en cuarto (ya sea creciente o menguante), la Tierra y el Sol forman un ángulo de 90º entre sí, vistos desde la Luna (esta es la causa de que veamos el terminador, i.e. la línea de separación entre la zona iluminada y no iluminada de la Luna, como una línea recta aunque ésta sea una esfera).
Con esto, y midiendo el ángulo que forman la Luna y el Sol vistos desde aquí (β en el dibujo de la izquierda), se podría obtener la relación entre las distancias Tierra-Luna y Tierra-Sol. Este ángulo le dio un valor de ~ 87º a las mediciones que efectuó Aristarco, lo que provocaba que la relación de las distancias fuera de ~20 (es decir, el Sol estaba unas 20 veces más lejos que la Luna).
Y puesto que ambos astros se ven desde la Tierra con el mismo tamaño aparente (si observamos el tamaño del Sol, es el mismo que el de la Luna al mirarlos desde aquí, de medio grado), significaría que el sol era 20 veces más grande que la Luna.
Lamentablemente, Aristarco cometió un gran error en la determinación de dicho ángulo, lo cual le llevó a ese resultado, cuando realmente el Sol está aproximadamente a unas 400 veces la distancia a la Luna, aunque eso no empaña su gran trabajo.
Al observar los eclipses lunares, esos donde la Tierra se interpone entre la Luna y el Sol y que acaban con nuestro satélite de un color rojizo, se observa cómo en la sombra rojiza que proyecta la Tierra sobre la Luna se distingue perfectamente el borde, 
redondo, con un diámetro bastante mayor que el de la Luna, el cual es básicamente el borde de la Tierra.
Cronometrando el tiempo que tardaba la Luna en entrar (o salir) de la sombra de la Tierra (es decir, desde que la sombra comenzaba a ocultar la Luna hasta que la tapaba completamente) y lo que duraba la fase de eclipse total (el tiempo que la Luna estaba oculta totalmente), se dio cuenta que el eclipse total duraba el doble que la “inmersión” de la Luna en la sombra (esto último duraba en torno a 1 hora), lo cual quería decir que el tamaño de la sombra tenía el doble del diámetro de la Luna.
A su vez, dado que la Luna avanzaba en una hora lo equivalente a un diámetro lunar, y dado que se conocía que la Luna tarda unos 29 días en recorrer toda la bóveda celeste (el tiempo que pasa entre dos lunas llenas, por ejemplo), quería decir que el camino que recorría era de unos 700 diámetros lunares.
Y esto, nos llevaba a que (por la famosa ecuación de que la longitud de una circunferencia de radio R es igual a 2*π*R) el radio de la órbita lunar (su distancia a nosotros vamos) era de algo más de unas 200 veces su diámetro.
Como se puede apreciar ya, Aristarco basó todo su procedimiento en ir encontrando relaciones entre las diferentes magnitudes (distancias y diámetros), lo que finalmente le llevó (utilizando triángulos semejantes para describir el sistema Luna-Tierra-Sol en el eclipse lunar) a poder determinar que el radio lunar era aproximadamente un tercio del radio de la Tierra (dato que cuenta con una más que razonable precisión).
Y esto, por las relaciones anteriores, implicaba que la Luna estaba a unos 20 radios terrestres (realmente está a unos 60), que el Sol se encontraba a unos 400 radios terrestres, y que el radio solar era unas 7 veces el terrestre (realmente es unas 100).
El gran error cometido en algunos de los datos se debe principalmente a la primera medida del ángulo que formaba la Luna con el Sol durante el cuarto, el cual tenía una gran complejidad de medida.
Y una vez llegados hasta aquí, ¿¡qué!?. Esto es lo que uno suele preguntarse al obtener resultados…
Afortunadamente, Aristarco no se quedó en solo esto sino que comenzó a razonar sobre dichos valores.
Acababa de obtener que el tamaño del Sol era bastante mayor que el de la Tierra y que el de la Luna. A su vez, ésta era más pequeña que la Tierra, aunque estaba mucho más cerca (por eso la vemos con el mismo tamaño aparente que el Sol).
Lo de la Luna tenía lógica, 
ya que como se pensaba, ésta estaba dando vueltas en torno a nosotros… pero no sucedía así con el Sol, ya que en este caso (según se creía en la época) el Sol estaba girando en torno nuestro a pesar de tener un tamaño mayor.
Claro que esto no encajaba muy bien dentro de la cabeza de Aristarco, por lo que dedujo que era más probable que el “cuerpo grande” fuese el que estaba quieto y el pequeño el que girase en torno a él, por lo tanto debería ser la Tierra la que girase en torno al Sol y no al revés.
Estas fueron las primeras ideas que sugerían que el modelo geocéntrico era erróneo… pero no fueron escuchadas en su momento (además de perderse en su mayoría), y se tuvo que esperar hasta 2000 años después para que otro hombre sacase a la luz ideas similares…
Accede a tu Zona Privada