Andrei Nikolaevich Kolmogorov nació el 25 de Abril de 1903, en Tambow cuando su madre se dirigía a Crimea. La madre María Yakovlena Kolmogorova murió en el parto y su hijo fue recogido en la casa de sus abuelos maternos por su tía, Vera Yakovlena. El padre de Kolmogorov, Nikolai Matveevich Kataev, un cualificado agrónomo y estadístico fue exiliado en Yaroslav. Después de la revolución socialista de octubre llegó a ser Director del Departamento de Educación en Narkomzem. Murió en 1919 en el frente sur durante la ofensiva de Denikin.
Kolmogorov paso los primeros años de su vida hasta 1910 cerca de Yaroslavl. A la edad de 5 años comprobó la ley:
1 = 12 , 1 + 3 = 22 , 1 + 3 + 5 = 32 , 1 + 3 + 5 + 7 = 42 , .....,1 + 3 + ...+(2n-1) = n2
Las primeras clases las tomo en una pequeña escuela que sus tías habían creado cerca de su casa, donde ellas (mujeres de altas ideas socialistas) seguían un método pedagógico muy avanzado para su tiempo. En esta escuela se editó la revista Spring Swallows donde publicó sus descubrimientos y algunos problemas aritméticos.
En 1910 junto con su tía se desplazo a Moscú, matriculándose en la escuela privada Repman Gymnasium (renombrada después de la revolución como Escuela de grado nº 23), donde encontró un ambiente intelectual medio que le fue de gran utilidad para su formación. En esta escuela se puso en práctica el premiar a los alumnos con unos escritos (especie de diploma en enseñanza superior) que ayudaban a potenciar la capacidad del alumnado. Kolmogorov obtuvo los correspondientes a Matemáticas, Biología e Historia de Rusia, y según el mismo, su ambición científica se debe a la profesores y al círculo de amigos que encontró en esta escuela.
Los últimos años de la escuela primaria no fueron fácil para él, ya que tuvo que trabajar junto con otros compañeros en la construcción de la vía férrea entre Kazan y Ekaterinburg (hoy Sverdlovsk), a la vez que se preparaba los exámenes de la escuela secundaria para poder obtener el titulo de grado secundario.
Después de obtener el grado en la escuela de secundaria en 1920, ingresó en la Facultad de Matemática y Física de Moscú, donde se admitía al alumnado sin realizar ningún tipo de examen. En ese momento tenían unos conocimientos básicos de matemáticas, adquiridos de la lectura del libro New Ideas in Mathematics. Al mismo tiempo ingreso en el Departamento de Metalurgia del Instituto de Tecnología y Química D. I. Mendeleiev, y continuo sus estudios de Historia en la Facultad de Historia de la Universidad, donde realizó su primer trabajo estudiando los siglos XV y XVI, para el análisis de los datos se apoyó en ciertas técnicas matemáticas, en particular los trabajos de Bayes.
El primer año (1920-1921) lo dedico a lecturas sobre la teoría de las funciones analíticas de N. N. Luzin y sobre geometría proyectiva de A. K. Vlasov. Destacar (por su posterior influencia) el hecho de que en el libro de Luzin se realizaba la demostración del teorema de Cauchy y se ponían ejemplos;
a la vista de la demostración, Kolmogorov remitió un contraejemplo de la demostración dada por Luzin, el cual tras comprobar la veracidad del contraejemplo (hoy se sabe que dicho contraejemplo también es falso) remitió un informe muy favorable sobre Kolmogorov al Seminario de Matemática donde estudiaba.
En el año siguiente ya era reconocido su talento matemático en Moscú. De la mano de P. S. Aleksandrov comenzó sus estudios en áreas más generales como "teoría de las operaciones sobre conjuntos", siguiendo y generalizando los estudios de Borel, Baire, Lebesgue,.. Sus trabajos en este tema , donde introdujo la noción del X operador-d S sobre unos conjuntos definidos, finalizaron en Enero de 1922, pero no fue hasta 1928 cuando se publicaron. Más tarde definió la noción de operación complementario para una operador X dado y probó diferentes resultados destacando el hecho de la existencia de conjuntos que no son borelianos.
En otoño de 1921 comenzó a trabajar en el seminario de V. V. Stepanov sobre series trigonométricas, donde resolvió el problema de la construcción de una serie de Fourier cuyos coeficientes tienden a cero mas lentamente de lo deseado, un problema en el cual Luzin estaba muy interesado. En el artículo resultante, el cual Kolmogorov describe como su primer trabajo en solitario, formula un resultado más completo sobre los valores de los coeficientes de Fourier. Cuando este trabajo llegó a manos de Luzin, quedo tan impresionado que le propuso que se fuese a trabajar con él. También obtuvo su más celebre resultado sobre series trigonométricas construyendo una serie de Fourier-Lebesgue que diverge casi para todo (en 1926 lo modificó ligeramente obteniendo un resultado más completo).
Su interés por la teoría de series trigonométricas y teoría descriptiva de conjuntos, hizo que sus investigaciones le llevaran al análisis clásico (diferenciación, integración, teoría de la medida y lógica matemática). Kolmogorov analizó en profundidad las afirmaciones y nuevas construcciones de la integral, buscando armonía y claridad a toda la teoría de integración, donde hasta ese momento los resultados habían sido generalizados sin ningún tipo de orden y conexión. Todos los trabajos realizados por él, en este sentido, aparecen en el primer volumen de sus trabajos que ya mencionamos.
En 1925 aparece sus primeros trabajos de lógica, donde intenta de una introducción a una amplia variedad de conceptos, donde destaca el hecho que las diferentes ramas de las matemáticas clásicas lleva consigo aparejado un armazón de intuición matemática que debería ser estudiada para ver la consistencia de sus afirmaciones.
En su cuarto año de universidad, en 1924, 
Andrei Nikolaevich Kolmogorov comenzó su interés en la rama de las Ciencias donde su nombre llegó a ser más importante La Teoría de la Probabilidad. Su primer artículo en esta nueva rama para él, "Über Konvergenz von Reihen, deren Glieder durch den Zufall bestimmt werden " data del 3 de Diciembre de 1925, y fue escrito en colaboración con A. I. Khinchin (también discípulo de Luzin). Este trabajo se componía de cuatro parte y Kolmogorov desarrollaba las tres últimas. Como el decía "todos mis trabajos en probabilidad con Khinchin en el periodo inicial describían los métodos de aplicación de la Teoría métrica de las funciones. Tales temas con las condiciones de validación de la ley de los grandes números y condiciones de independencia de series de variables aleatorias independientes eran abordados por los métodos descritos por N. N. Luzin y sus pupilos, en la teoría general de series trigonométricas". De esta época es la clásica desigualdad de Kolmogorov :
" Si h 1 , h 2 ,.... son v. a. independientes, Eh i = 0 , Sk = h 1 + .... + h k , entonces:
La desigualdad es hoy conocido de la siguiente forma:
" Si h 1 , h 2 ,.... son v. a. independientes, Eh i = 0 , P(ú h kú £ C ) =1, k =1,....,n, entonces:
De esta colaboración en la Teoría de la probabilidad hemos heredado el teorema y el criterio de Kolmogorov-Khinchin.
En 1925 Kolmogorov se gradúa y realiza los estudios de postgrado, bajo la supervisión de Luzin. Sus trabajos sobre las condiciones de la ley de los grandes números y la ley fuerte de los grandes números se realizaron entre 1927-1929. A finales de 1927, había completado sus investigaciones sobre suficiencia y condiciones necesarias y suficientes de la ley débil de los grandes números, comenzadas por J. Bernouilli y continuada por P. L. Chebyshev y A. A. Markov. El 24 de Diciembre de 1927, obtiene las condiciones necesarias y suficientes de la ley generalizada de los grandes números para series. Más tarde en 1930 obtiene otro famoso resultado ahora incluido en cualquier libro de probabilidad, La ley fuerte de los grandes números:
" Si x 1 , x 2 , ...es una sucesión de v. a. independientes con momentos de segundo orden finito y
.
(Dx indica varianza de x) entonces: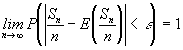 
para cualquier e>"
En 1933 remarcó este hecho para el caso de v. a. independientes e idénticamente distribuidas, que es fácilmente deducible a partir del anterior. Aunque el término de "ley fuerte de los grandes números" fue introducido por Khinchin (1927-1928), el cual demostró ciertas condiciones para su validación y lo aplicó también al caso de dependencia; fue el trabajo de Kolmogorov para v. a. independientes donde se da una completa formulación del problema y una demostración muy clara.
En Mayo de 1929 finaliza su cuarto año de estudiante de postgrado, con 18 artículos publicados desde 1923 a 1928. Así en junio de 1929 entra a formar parte del Instituto de Matemáticas y Mecánica de la Universidad de Moscú, el cual a partir de ahora será un fuerte punto de apoyo de todos sus trabajos e investigaciones.
A finales de los años 20 y principios de los 30 la actividad creativa de Kolmogorov en diferentes ramas de las matemáticas (simultáneamente) fue muy importante.
En 1929 publicó "La Teoría general de la medida y el cálculo de probabilidades " donde da la primera versión de su axiomática constructiva de la fundamentación de la Teoría de la probabilidad, la cual posteriormente llegó a conocerse como " La axiomática de Kolmogorov " descrita en "Grundbegriffe der Wahrscheinlichkeitsrechnung" (1933). Kolmogorov dijo : "La axiomática de la probabilidad debe estar construida sobre las bases de la teoría general de la probabilidad y teoría métrica de las funciones. El comportamiento de la teoría a partir de los estudios de propiedades de las funciones dependen exclusivamente de la medida de los conjuntos cuando las funciones toman este o aquel conjunto de valores". Él habla de "el espacio de los sucesos elementales de un problema dado y la probabilidad de conjuntos de estos elementos".
Ya en el año 1909, Borel consideró la importancia de la teoría general de la medida para la construcción de la fundamentación de la teoría de la probabilidad, pero no es sin embargo hasta 1933, (cuatro años después de aparecer el artículo "La teoría general de la medida y el cálculo de probabilidades"), cuando Kolomogorov publicó la clásica monografía "Grundbegriffe der Wahrscheinlichkeitsrechnung" (1933), donde da forma a la idea inicial de Borel. Esta monografía llego a ser la base de todos los trabajos posteriores en teoría de la probabilidad.
En la introducción de Los Fundamentos de la Teoría de la Probabilidad (la edición en ruso aparece en 1936 y la edición en inglés en 1950) Kolmogorov hace notar algunos aspectos muy importante:
El significado de todos estos resultados y la utilidad de la axiomática es muy clara hoy, mucho más de lo que fue hace 63 años cuando se publicó.
Desde junio del 1930 a marzo de 1931 estuvo de viaje por Francia y Alemania, y a su vuelta fue nombrado profesor de la Universidad de Moscú. Además de ser nombrado Director del Instituto de Ciencias e Investigación en Matemáticas, en Diciembre de 1933, donde permaneció hasta el 15 de Abril de 1939 (retornando por un breve periodo en 1951-1953).
En 1936 y 1937, Kolmogorov realiza un trabajo intensivo sobre el comportamiento asintótico de las probabilidades de transición de las cadenas de Markov sobre espacio de estado numerable. La amplitud de los trabajos y su interés científico se muestra en sus aplicaciones, cuando aplica el cálculo de probabilidades a problemas de biología, genética, física, geología, ...Así en su artículo "Sobre la solución de un problema biológico" trata con un modelo simple de un proceso aleatorio, encontrando el comportamiento asintótico de la probabilidad de extinción cuando se incrementa el número de generaciones. En 1939, escribe un artículo donde apoyándose en los datos de N. I. Ermolayeva, aporta un estudio riguroso sobre la veracidad de las leyes de genética de Mendel.
En un breve esbozo de los artículos publicados por Kolmogorov en los años 30 sobre diferentes ramas llegamos a contabilizar: 1931-5 artículos, 1932-6, 1933-9, 1934-10, 1935-4, 1936-17, 1937-9, 1938-16 y 1939-5. Por supuesto el campo de trabajo que más destaca es el referente a la teoría de la probabilidad.
El 29 de Enero del 1939 fue elegido miembro de la Academia de Ciencias URSS, donde ocupo el cargo de secretario en el Departamento de Física y Matemáticas desde 1939 a 1942, y fue miembro del Presidium de la Academia de Ciencias de URSS. Desde 1938 a 1958 encabezó el Departamento de Probabilidad en el Instituto de Matemáticas Steklov, Academia de Ciencias URSS.
A finales de los años 30 y principio de los 40 los trabajos de Kolmogorov en la teoría de los procesos aleatorios con incremento estacionario y la teoría relativa a turbulencias isotrópicas, fueron extraordinarios tanto en el aspecto conceptual como por la profundidad de sus ideas y en el aspecto de sus aplicaciones. En particular sus resultados juntos con los de Wiener crea una nueva rama en la teoría de los procesos aleatorios, con amplias aplicaciones en ciencias e ingenierías.
En este periodo, y dentro de sus trabajos sobre turbulencias, formula su famosa "ley de dos tercios" que decía que : "la media cuadrática de la diferencia de velocidades en dos puntos, localizados a distancia r (no demasiado grande ni demasiado pequeño), es proporcional a r2/3 "
Kolmogorov era una persona muy responsable y cuidadosa tanto en sus estudios como matemático puro, como en su aspecto práctico, de aplicaciones de sus investigaciones. Poseía un gran capacidad para penetrar dentro de la esencia de cada problema y seleccionar los aspectos básicos, expresando claramente las diferentes posibilidades intrínsecas en cada uno de ellos. Como ejemplo de ello tenemos el artículo escrito en 1949 , "La solución de un problema de probabilidad relacionado con la formación de estratos".
En vísperas de la segunda guerra mundial realizó diferentes trabajos sobre la teoría balística, ya que se le pidió que estableciera una discusión dentro de su departamento sobre algunos temas relacionados con la artillería: ¿cómo estimar la medida de exactitud de datos experimentales?. En colaboración con el Instituto de Investigaciones de la Marina, Kolmogorov emprendió una profunda investigación sobre teoría y práctica (cálculos computacional) de la eficiencia en los sistemas de tiro.
En 1946 aparece el libro de H. Cramer, "Métodos Matemáticos de la Estadística". En su versión en ruso, Kolmogorov escribe la introducción destacando el trabajo de Cramer. A raíz de este libro, estimuló a sus compatriotas a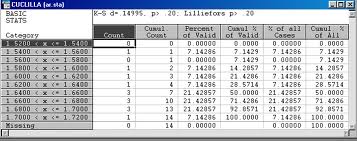 
que trabajaran sobre investigación estadística. En relación con lo anterior, Kolmogorov escribió dos informes en la Segunda Conferencia de Estadística Matemática, Tashkent, 1948: "Problemas básicos de estadística teórica" y "El significado real del análisis de varianza". En Marzo de 1950 completó uno de sus trabajos más importante en Estadística: "Estimadores Insesgados", donde analiza sistemáticamente las propiedades de los estimadores insesgados y los diferentes métodos de construcción, por medio de estadísticos suficientes, y también describe el significado de las aplicaciones de estos estimadores en problemas de estadísticas de control y control de calidad en la industria.
De 1949 es el libro "Distribuciones Limites para Sumas de Variables Aleatorias Independientes" que Kolmogorov junto con B. V. Gnedenko aportaron a la Teoría de la Probabilidad, dedicado a la teoría de los teoremas límites, cuyo centro es la noción de ley infinitamente divisible y ley de estabilidad. En su introducción al libro se describen los problemas de teoremas límites que les llevo a esas leyes como sigue:
" Si x 1 , x 2 , ... es una sucesión de variables aleatorias independientes idénticamente distribuidas, Sn = x 1 +...+ x n , entonces es natural preguntarse acerca de las condiciones bajo
las cuales el límite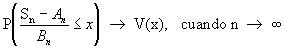 
manteniendo la misma elección de An y Bn , y cual es la distribución límite V(x) que surge de aquí " ( El problema completo fue resuelto por Khinchin ).
A finales de los 40 comienza un trabajo muy importante en La Gran Enciclopedia Soviética (2ª Edición), como responsable de la sección de matemáticas. Realizó el glosario, selecciono los trabajos, editó artículos y también hizo contribuciones en diversas ramas de las matemáticas. De todas sus aportaciones a la enciclopedia debemos destacar especialmente su famoso artículo "Mathematicas", donde brevemente perfiló la historia de las matemáticas.
De este periodo destacar los siguientes premios:
A finales de 1942 se casó con Anna Dmitrievna Egorova, una amiga desde la escuela.
En este periodo las ramas matemáticas a las cuales van dirigidas sus investigaciones y que están asociadas inseparablemente con su nombre cuando surgen en los ambientes científicos y de estudios son:
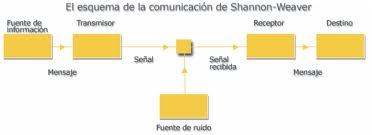
En 1956 elabora un informe sobre "La Teoría de transmisión de información " para una sesión de la Academia de Ciencias de URSS dedicada a los problemas científicos en la industria de la automatización. El informe contenía los conceptos básicos de la teoría de la información y sobre todo clarificaba los límites de aplicación de ésta. A partir de los estudios de Shannon respecto a la entropía, y definió la e -entropía He (x ) de un variable aleatorio x como
He (x ) = inf I(x ,h ),
donde el ínfimo es tomado sobre todos los pares de variables aleatorias (x ,h ) los cuales cumplen que su distribución conjunta Px ,h pertenece a una clase dada We , dependiente de un parámetro e . También introduce el concepto de e -entropía relativa He (C,X) y determina su logaritmo binario Ne (C,X) del número mínimo de elementos en un nodo-e desde X al conjunto C. De hecho, los valores He (C) y He (C,X) se construyen generalmente de la misma forma que los llamados "diámetros de Kolmogorov " introducidos por él en 1936. De su noción y posterior desarrollo de la e -entropía se entra en una nueva rama de investigaciones en la teoría de la aproximación.
Respecto a la aportación a la estadística en este periodo, se siente influenciado por los trabajos de Yu. V. Prokhorov (alumno y discípulo suyo) sobre el cálculo de una función de distribución arbitraria para una sucesión de funciones de distribución Dn , bajo determinadas condiciones. Destacando su trabajo sobre " Dos teoremas de límite uniforme para las sumas de variables aleatorias independientes" (1956) y "Sobre la aproximación de distribuciones de sumas de términos independientes por distribuciones infinitamente divisibles ".
En los años 50 aporta a la probabilidad una nueva rama en la teoría de los procesos aleatorios, la teoría de los teoremas de límites funcionales (en particular los del "principio de invarianza") cuyos fundamentación se debe a los trabajos realizados por él junto con Prokhorov y Skorokhod. Este problema ya lo venía abordando desde 1931, sobre todos los referidos a los problemas típicos de restricciones para el principio de invarianza. En 1948 realizó un informe para la Sociedad Matemática de Moscú, "Medidas y funciones de probabilidad en espacios funcionales", donde sugiere considerar la distribución de un proceso aleatorio como una medida en un s -álgebra de Borel para algún espacio funcional, y por supuesto considerar la convergencia débil de las distribuciones como la convergencia puntual en un espacio de medida. Las ideas básicas de la teoría general de convergencia débil de las medidas de probabilidad sobre un espacio métrico y sus resultados fueron presentado en un informe conjunto de Kolmogorov y Prokkhorov en la Conferencia sobre Probabilidad y Estadística Matemática de 1956 (Berlín).
Respecto a otras actividades no investigadora, hay que destacar que de 1951 a 1953 fue Director del Instituto Científico e Investigador en Matemáticas y Mecánica de la Universidad Estatal de Moscú. Durante 4 años (1954-1958) 
fue Decano de la Facultad de Matemáticas y Mecánica de la Universidad Estatal de Moscú, responsable del Departamento de Probabilidad de esta Facultad (desde 1939 a 1966) y jefe de la División de Probabilidad del Instituto de Matemáticas Steklov, Academia de Ciencias de la URSS (desde 1939 a 1958).
En este periodo los principales trabajos de Kolmogorov se basan sobre todo en las fundamentaciones lógicas de la teoría de la información, de la teoría de la probabilidad y su reconstrucción sobre una base algorítmica. Hay que destacar que, como en los años 50, cuando los esfuerzos de Kolmogorov estaban concentrados en las aplicaciones de la teoría de la información a diferentes ramas de las matemáticas, esta vez desarrolló dos nuevas:
Estos nuevos conceptos fueron introducidos e investigados por Kolmogorov en sus artículos, "Tres aproximaciones a la definición de cantidad de información" (1965), "Una fundamentación lógica de teoría de la información y del cálculo de probabilidades" (1969) y "Fundamentación combinatoria de la teoría de la información y el cálculo de probabilidades" (1983).
En 1960-61 escribe un nuevo método para estimar la consistencia de la entropía del lenguaje, sugiriendo en 1962 una aproximación combinatoria pura: la entropía del lenguaje combinatoria es definida como el límite --7--
donde Nn es el número de textos de longitud n compuestos de palabras de un vocabulario dado y obedeciendo unas reglas gramaticales dadas.
Siguiendo con el estudio del lenguaje, los trabajos de Kolmogorov y sus discípulos se podrían dividir en tres grupos: Relacionados con las leyes métricas, la clasificación y estadísticas de las variedades rítmicas de la métrica y el análisis de la entropía residual y sus limitaciones.
La actividad científica y organizativa en este periodo queda señalada por dos grandes acontecimientos: la creación del Laboratorio de Métodos Estadísticos, en el Departamento de Probabilidad de la Facultad de Matemática y Mecánica (Universidad Estatal de Moscú) y de la Escuela de Matemáticas y Física ( nº 18 ), con el patrocinio de la Universidad Estatal de Moscú. El primero de ellos, con Kolmogorov como Director, se creó con el fin de unificar esfuerzos e intensificar las investigaciones en las aplicaciones de la probabilidad y los métodos estadísticos. Es interesante destacar que dentro de esta organización, e influenciado por los trabajos de J. Neyman, Kolmogorov se interesó por el análisis estadístico de los fenómenos atmosféricos, mostrando que los métodos paramétricos de Neyman eran demasiado sofisticados (no robustos) para los toscos datos atmosféricos. Conectando con ello desarrolló sus métodos de test no paramétricos (completando los conceptos dados años antes por Fisher .
El 25 de Abril de 1963, el Presidium del Soviet Supremo de la URSS concede el grado de Académico Avanzado a A. N. Kolmogorov con el título de "Héroe del Trabajo Socialista".
En 1963 recibió el Premio Internacional en Matemáticas por la Fundación Internacional Balzan. En 1965, junto con V. I. Arnold, fué premiado con el Premio Lenin por sus trabajos en la teoría de las perturbaciones de sistemas Hamiltonianos.
El progreso en las escuelas de matemáticas es el eje central de las actividades de Kolmogorov en este periodo. En su trabajo de escuela, crea una popular revista científica en física y matemáticas para chicos de escuela, Quantum, de la que es el Director.
Podemos realizar una escueta trayectoria de sus últimos años como sigue:
Al principio de los años 80, el Presidium de la Academia de Ciencias de la URSS decide publicar una selección de sus trabajos. Kolmogorov realiza una lista de los artículos que desea incluir agrupados por temas, escribe sus comentarios y completa sus trabajos con un comentario general sobre los artículos escritos por sus discípulos.
El 20 de Octubre de 1987, a los 84 años de edad, Andrei Nikolaevich Kolmogorov falleció. Como premio a su pródiga vida la comunidad científica le otorgó infinidad de premios entre los que destacamos:
Accede a tu Zona Privada