Lamentablemente para la Física y la Astronomía, con Aristóteles que, como todos los filósofos griegos, ambicionaba explicar todos los fenómenos, la especulación mitiga prácticamente toda su labor en esta área.
Pese a ello, y puede decirse que, en perjuicio de la ciencia, la influencia aristotélica perduraría más de dos mil años, aunque no es imputable a este gran filósofo, sino al dogmatismo 
y falta de espíritu crítico que reinó durante la Edad Media, en que si un hecho no aparecía en textos de Aristóteles había de ser falso.
El siguiente paso, o necesario desarrollo, para el progreso de la Astronomía, acontece en la Geometría. La geometría esférica fue desarrollada por muchos matemáticos, sobre el 330 a.c., Autólico, sabio griego que pone nombre a uno de los cráteres lunares, basándose en un escrito anterior de Eudoxo, trabaja sobre la esfera en movimiento.
Alejandro Magno funda, y a su muerte en 323 a. c, Ptolomeo I (no confundir con el astrónomo cuya obra es el punto de inflexión de la herencia astronómica griega), continúa la construcción de la ciudad que pasa a ser no sólo la capital del Imperio, sino también el centro de la vida intelectual y científica, Alejandría (actual Egipto).
Modelada según el ideal griego, su situación geográfica y su puerto al Mediterráneo, la hacía centro ideal de comunicaciones comerciales, amén de constituir un magnífico centro estratégico.
Se crea en Alejandría el Museo o Templo de las Musas, inspirado en el modelo del Liceo aristotélico. Se convirtió en un centro de investigación y enseñanza al que se puede otorgar el título de primera universidad del mundo.
Se componía de cuatro departamentos: literatura, matemáticas, Astronomía y medicina, estando al frente de cada uno de ellos un director. Disponía de la mayor biblioteca que se conoció en la antigüedad (su fondo inicial fue el del Liceo de Aristóteles), llegando a contar con más de medio millón de ejemplares.
Tenía aulas de enseñanza y salas de estudio, laboratorios para la investigación, observatorio astronómico, jardín botánico y un zoológico.
El Museo supervivió durante seiscientos años, si bien tuvo su mayor esplendor durante los siglos III y II a.c. La filosofía helénica ya no pudo igualar su anterior brillantez, sin embargo las matemáticas y la física alcanzaron cotas admirables.
Allí Euclides, trabajó y escribió sobre geometría en general y también hizo una importante contribución a la geometría esférica de Autólico. Escribió Phaenomena, una introducción elemental a la astronomía matemática y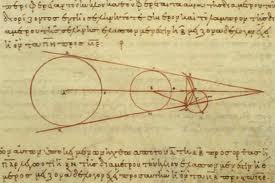 
da resultados sobre el momento en que las estrellas en ciertas posiciones saldrán y en el que se ocultarán. En este período se originan los sistemas de coordenadas para dar las posiciones estelares.
Tanto el sistema ecuatorial como el eclíptico, al aparecer estos sistemas, se dan como resultado de la necesidad de tener mediciones más precisas.
Arquímedes «el defensor de Siracusa» (287 - 212 a.c.), construyó en Alejandría un planetario, que mostraba con gran precisión los movimientos de los principales cuerpos en el cielo y reproducía eclipses. Desarrolló el cuadrante para estudio astronómico y un aparato para medir el ángulo entre el Sol y la Tierra.
En Astronomía hay que destacar a Aristarco, Eratóstenes e Hiparco.
Aristrarco de Samos nació en el año 310 a.c. y, aunque no vivió en Alejandría, se le puede considerar alejandrino por su espíritu e influencia. Educado por un discípulo de Aristóteles, sus descubrimientos llegaron inmediatamente a Alejandría y sus escritos fueron profusamente divulgados.
En su tratado Sobre los tamaños y distancias del Sol y la Luna, elabora un método para calcular las proporciones entre las distancias de la Tierra al Sol y a la Luna de un destacable ingenio.
Acepta la teoría de Anaxágoras sobre las fases de la Luna. Dice, ‘cuando la Luna está en cuarto cuadrante o cuarto menguante, el ángulo que forma ésta con el Sol y la Tierra es de 90°’. Midió el ángulo que forma en esas circunstancias la Tierra con la Luna y el Sol, y, por comparación con otros triángulos semejantes, dedujo que la distancia de la Tierra al Sol era veinte veces la de la Tierra a la Luna.
Aunque la proporción entre ambas distancias es en realidad de cuatrocientos, el error cometido no proviene del método utilizado, que es correcto, sino de los instrumentos de medida de que disponía, ya que el ángulo que midió fue de 87°, siendo el ángulo real de 89° 51’.
En el mismo tratado asevera: «Cuando el Sol está totalmente eclipsado, el Sol y la Luna están comprendidos en un mismo cono, que tiene su vértice en nuestros ojos», concluye que el diámetro del Sol debe ser veinte veces mayor que el diámetro lunar (de nuevo incurre en el mismo error de medida).
Siguiendo su interés en conseguir unas proporciones adecuadas del Universo, aprovechó un eclipse de Luna y, cronometrando el tiempo que tarda en pasar la Luna a través de la sombra de la Tierra, estimó que el diámetro de ésta es el doble que el de la Luna (en realidad es cuatro veces mayor).
No llegó a calcular ninguna distancia absoluta, pero en una época en la que afirmar que la Luna era tan grande como el Peloponeso era peligroso, el intuir las proporciones del universo es meritorio.
Defendió que la Tierra no está fija, sino que realiza dos movimientos: uno alrededor del Sol, al igual que los demás planetas, y otro sobre su eje norte-sur.
Comprendió que su teoría del sistema heliocéntrico, iba a encontrar grandes problemas, por enfrentarse a las enseñanzas de Platón y Aristóteles, pero también porque, para la religión, «contradice a los dioses y ofende su dignidad», incluso a la apreciación «de sentido común», ya que, a simple vista, parece que es el Sol el que gira en torno a la Tierra.
La formulación de la teoría heliocéntrica encierra un interesante problema: «si la Tierra se mueve y las estrellas están quietas, éstas tienen que presentar distintas posiciones relativas». 
Para comprender esta objeción sirva ser usado un ejemplo: un barco que navega cerca de la costa y que en un instante determinado se ve desde él una casa y a continuación un árbol. A medida que el barco se vaya desplazando y pasado un cierto tiempo, el objeto que aparecerá en primer lugar será el árbol, quedando la casa detrás de él. Este fenómeno, conocido con el nombre de 'paralaje', que no pudo ser observado sino hasta el siglo XIX, con superiores aparatos de medición, no lo apreciaremos si la distancia del barco a la costa es muy grande. Pues la misma explicación daba Aristarco, disponiendo que la distancia de las estrellas a la Tierra es tal que el diámetro de ésta es despreciable frente a aquélla.
Resulta así que esta representación heliocéntrica tenía una ventaja inmediata: permitir a los planetas aproximarse a la Tierra en unas ocasiones y en otras alejarse, dando una explicación a las observaciones, de otro modo inexplicables, de la variación del brillo de los planetas durante el año.
Pero el mundo antiguo vió serios inconvenientes en la hipótesis de Aristarco.
El punto en que se encontraba la investigación astronómica, cuando ya eran conocidas ciertas proporciones y estaba elaborado un modelo descriptivo bastante aproximado a la realidad, requería dar un paso: el cálculo de dimensiones y distancias absolutas.
Este salto lo dió Eratóstenes (275-194 a.c.), realizando una gran proeza, indicó el tamaño dela Tierra, midiendo su radio.
La primera medición científica de una distancia cósmica fue realizada por él, hacia el año 240 a.c, apreció que el 21 de junio, cuando el sol, al mediodía, se hallaba en su cénit en la ciudad de Siena (Egipto), no lo estaba también, a la misma hora, en Alejandría, unos 750 km al norte. Concluyó que la explicación debía de residir en que la superficie de la Tierra, al ser redonda, estaba siempre más lejos del Sol en unos puntos que en otros.
Tomando por base la longitud de la sombra de Alejandría, al mediodía en el solsticio, la ya avanzada Geometría pudo responder a la pregunta relativa a la magnitud en que la superficie de la Tierra se curvaba en el trayecto de los 750 km entre Siena y Alejandría. A partir de este valor pudo calcularse la circunferencia y el diámetro de la Tierra, supo-niendo que ésta tenía una forma esférica, hecho que los astrónomos griegos de entonces aceptaban sin vacilación. Eratóstenes hizo los correspondientes cálculos, sus cifras fueron, aproximadamente, de 12.000 km para el diámetro y unos 40.000 para la circunferencia de la Tierra. Así pues, aunque quizá por casualidad, el cálculo fue bastante correcto.
Eratóstenes hizo las siguientes hipótesis, hoy se sabe incorrectas pero tan aproximadas que le dieron un resultado exacto en la medición:
• La Tierra es esférica.
• Los rayos de Sol son paralelos cuando chocan sobre la Tierra (lo que significa que el Sol está muy alejado de la Tierra).
• Los dos lugares de la superficie terrestre donde hizo sus observaciones: Alejandría y Siena (Egipto), están en la misma línea Norte-Sur.
• Siena se halla exactamente sobre el trópico del Cáncer(latitud 23 ½ ° N) de tal modo que el Sol está directamente sobre la cabeza, a medio día, el día de Solsticio de verano.
Eratóstenes midió también el ángulo de la eclíptica, realizó un mapa de la parte conocida de la Tierra y creó uno de los calendarios más avanzados para su época y una historia cronológica del mundo desde la guerra de Troya, fué de hecho el autor del calendario juliano (impuesto por Julio César en el 45 a.c.), formado por 365 días y un año bisiesto de cada cuatro (un error de tres días cada cuatrocientos años).
Fue probablemente Eratóstenes quien diseñara la ‘esfera armilar’, un astrolabio para mostrar el movimiento aparente de las estrellas alrededor de la Tierra.
Tras ellos, Hiparco (190-120 a.c.). Estudió en Alejandría. Entre sus aportaciones cabe destacar: el primer catálogo de estrellas, la división del día en 24 horas de igual duración, el descubrimiento de la precesión de los equinoccios, la distinción entre año sidéreo y año trópico, mayor precisión en la medida de la distancia Tierra-Luna
y de la oblicuidad de la eclíptica.
Disponía de los informes realizados en el Museo, así como de las observaciones de los astrónomos anteriores, en las que se apoyó para su mayor descubrimiento, que el punto alrededor del cual giran las estrellas, es decir, el polo celeste, varía con el tiempo. Lo que realmente aporta tal hallazgo es que el eje de rotación de la Tierra describe un cono. Aunque Hiparco defendía la teoría geocéntrica (la Tierra en el centro del Universo), lo hizo teniendo en cuenta que sus observaciones no satisfacían la teoría heliocéntrica tal y como estaba expuesta en ese momento.
Hiparco se propuso el siguiente planteamiento: Si el Sol gira con una trayectoria circular, estando la Tierra en el centro, y el movimiento circular del Sol es uniforme, entonces, dados unos ángulos resultarán iguales, y su valor de 90° (el razonamiento será análogo suponiendo que es la Tierra la que gira).
Midió dichos ángulos y comprobó que no eran iguales, luego la distancia Tierra-Sol varía. Esto le hizo suponer que la Tierra estaba algo desplazada del centro de giro del Sol.
(Este problema será resuelto por Kepler, al plantear que la Tierra gira alrededor del Sol formando una elipse, estando éste situado en uno de los focos de la elipse).
En el año 134 a.c. apareció una nueva estrella en el cielo, este hecho no pasó inadvertido a Hiparco; su espíritu crítico le hizo anotarlo, si bien el suceso iba en contra de la inmutabilidad aristotélica de los cielos. A partir de este momento, su idea de realizar un mapa celeste lo más perfecto posible le preocupó aún más. Hiparco era consciente de la importancia y utilidad de disponer de los antiguos mapas babilónicos.
Además de un catálogo de 1.080 estrellas, reunió numerosos datos de los movimientos de la Luna y los planetas para que sus sucesores construyeran el modelo que los pudiera interpretar. Esto es, aceptar que un solo individuo no es sino un eslabón en el conocimiento científico.
La Astronomía y la Física necesitaban que se creara la Trigonometría. Tales dió el primer paso enunciando la semejanza de triángulos, Aristarco y Arquímedes lo ampliaron, pero es Hiparco quien dió el salto cualitativo que se requería. Publicó una tabla de ángulos y cuerdas, ejemplo de una tabla trigonométrica, cuyo propósito era proporcionar un método para resolver triángulos.
En la segunda mitad del siglo II a.c., la prosperidad económica de Alejandría y de todo el oriente helénico empieza a decaer.
Roma, como nueva potencia, comienza a imponer su autoridad, pasa a ser capital, aun cuando Alejandría continúa siendo la cuna del saber, aunque los intelectuales de la época pierden el impulso anterior.
En este momento surge la figura de uno de los más importantes astrónomos de la historia…
Claudio Ptolomeo (85-165 de nuestra era), supo sistematizar la Astronomía griega al igual que siglos atrás hiciera Euclides en matemáticas. Vivió e hizo sus observaciones y estudios en Alejandría. No se distinguió ni como observador ni como teórico, 
pero tuvo el mérito de recopilar en un extenso tratado todos los conocimientos astronómicos de su época.
Su doctrina es conservadora pues utiliza el sistema geocéntrico, desarrollo la teoría de los climas, y resolvió los problemas trigonométricos de la Astronomía mediante las cuerdas del arco doble.
En sus libros siempre se apoya en ejemplos experimentales para explicar sus teorías, dándoles un talante científico, por tanto alejándose de anteriores razones mágicas.
Afirma que los planetas describen órbitas circulares llamadas 'epiciclos' alrededor de puntos centrales que a su vez orbitan de forma excéntrica alrededor de la Tierra. Por tanto la totalidad de los cuerpos celestes describen órbitas perfectamente circulares, aunque las trayectorias aparentes se justifican por las excentricidades. Mejoró el catálogo estelar a 1.028 estrellas.
Su libro más importante es 'El Almagesto', que serviría de texto durante la Edad Media, y representa la culminación de todos los esfuerzos de la antigüedad por defender el sistema geocéntrico.
Recogió la mayoría de los conocimientos astronómicos griegos anteriores a él, especialmente los de Hiparco y de los babilonios.
También en su obra merece destacar:
- El Tetrabiblos, cuatro libros que se refieren al influjo ambiental, a las fuerzas de acción de los planetas, signos y estrellas, a los gobiernos geográficos y al horóscopo individual y colectivo.
-Geografía, determina las diversas regiones desde el punto de vista de su posición astronómica, mas que topográfica.
- Armonicos, analiza comparativamente lo fundamentos de la música pitagórica y la griega de su tiempo. Aplica la teoría general de la música de las esferas a los aspectos astrológicos.
El resultado es un extremadamente complicado sistema, tomando y desechando diferentes teorías de Platón y Aristóteles, en el cual excéntricas, epiciclos y deferentes se entrelazan caóticamente en un desesperado intento por reproducir los movimientos planetarios sin violar la rígida norma de trayectorias circulares.
Todavía se hace uso del movimiento circular uniforme y de la Tierra en reposo. No se hace hincapié en el esquema de esferas rotatorias, todas concéntricas con la Tierra, sobre las que se hallan fijos el Sol, la Luna y los planetas. No se requiere que todas las rotaciones tengan como centro la Tierra.
Esta complejidad se hace aún más evidente cuando vemos que Ptolomeo tuvo necesidad de añadir otro artificio (el 'ecuante') para representar o justificar, de modo más adecuado, ciertas características del movimiento de algunos planetas.
Efectivamente, el modelo que presenta Ptolomeo incluye el movimiento excéntrico, en epiciclos y el ecuante:
Esta teoría se ajustaba muy bien a las observaciones de su época y resultó útil para los astrónomos y navegantes durante varios siglos después.
Sin embargo, aumentaba en dificultad
cada vez que se perfeccionaban los aparatos de medida, llegando en el siglo XVI a necesitarse 70 movimientos simultáneos para justificar el esquema ptolomeico.
En su ‘gran obra’ el mencionado Almagesto (nombre otorgado por las traducciones árabes) estableció las siguientes hipótesis:
• Que el cielo es de forma esférica y tiene un movimiento de giro.
• Que la Tierra, considerada como un todo, es también de forma esférica.
• Que está situada en medio del cielo como su centro.
• Que por razón de sus dimensiones y distancia a las estrellas fijas, la Tierra se comporta frente a esta esfera como si fuese un punto.
• Que la Tierra no participa de ningún movimiento.
En muchos aspectos estaba de acuerdo con la doctrina filosófica y física de los griegos relativa a la naturaleza de la Tierra y de los cuerpos celestes y tenía, de hecho, una apariencia de sentido común, ver al Sol y la Luna moverse mientras uno permanece dota de sentido la sensación de que la Tierra fuere plana.
Con Ptolomeo, la Física y la Astronomía griega llegaron a su fin.
Su sistema geocéntrico de la Tierra no será sustituido hasta el heliocéntrico de Copérnico. Sólo Tycho Brahe propuso un sistema intermedio, con la Tierra como centro, circundada por la Luna y el Sol, 
y este a su vez se ve circundado por los planetas.
El dominio romano sobre el imperio helénico, destruyendo su libertad e impidiendo desarrollar sus aspiraciones nacionales. Roma no tenía inquietudes científicas.
En lo que concierne a la ciencia, el Imperio romano, dejó apenas algún testimonio, por ejemplo, Lucrecio en su poema, De Natura Rerum, ‘sobre la naturaleza de las cosas’, expuso su visión materialista y evolutiva del Universo.
En Astronomía no hubo algún descubrimiento de importancia capital, desde Ptolomeo, hasta Copérnico.
El hombre había perdido el afán de saber, va a volver los ojos al cielo en términos religiosos, pero no mira ya las estrellas.
Accede a tu Zona Privada
